Varianza y desviación estándar de datos agrupados de variable discreta
Si trabajamos con una tabla de frecuencias con datos agrupados de una variable discreta, es decir, la variable toma valores puntuales, no intervalos de valores, podemos calcular la varianza y la desviación estándar usando las fórmulas que veremos en esta clase.
Veamos los ejemplos y ejercicios que hemos preparado.
Fórmulas para la varianza y desviación estándar de datos agrupados

Donde:
- fi: frecuencia absoluta de cada valor, es decir, número de veces que aparece el valor en el estudio.
- xi: valor de los elementos de la población.
- σ2: varianza de la población.
- σ: desviación estándar de la población.
- μ: media poblacional.
- s2: varianza de la muestra.
- s: desviación estándar de la muestra.
- x̄: media de la muestra.
- k: número de clases.
Tenemos siempre que fijarnos si estamos trabajando con datos que forman una población o con datos que forman una muestra, pues las fórmulas son diferentes.
Podemos ver también que la fórmula de la varianza se presenta de 2 formas diferentes, puedes tomar cualquiera de ellas, obtendrás el mismo resultado.
En los problemas, seguiremos los siguientes pasos:
- Calculamos el número de elementos.
- Calculamos la media.
- Calculamos la varianza.
- Calculamos la desviación estándar, que es la raíz cuadrada de la varianza.
Ejemplo 1:
Calcular la varianza y la desviación estándar de las edades de una población de niños que asisten a una fiesta infantil.

Solución:
Para calcular la varianza y la desviación estándar, empezamos calculando el número de elementos de la población:

En la tabla, sumamos las frecuencias fi:
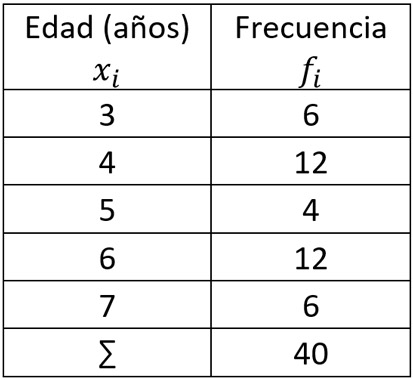
Y así obtenemos el número de elementos de la población (N).
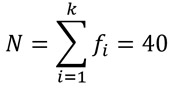
A continuación, calculamos la media poblacional partiendo de su fórmula:

En la tabla de frecuencias agregamos la columna xi · fi

Ahora sí, calculamos la media poblacional:
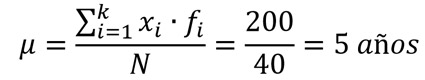
A continuación, recordamos la fórmula de la varianza de la población:
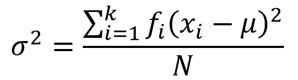
En la tabla, agregamos 3 columnas más, para buscar la expresión de la fórmula:

Usamos la fórmula:
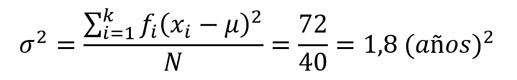
El valor de la varianza de esta población es de 1,8 (años)2. Ten en cuenta que la varianza queda expresada en las unidades originales elevadas al cuadrado, por ello, nos quedaría en (años)2.
Finalmente calculamos la desviación estándar, teniendo en cuenta que es la raíz cuadrada positiva de la varianza:
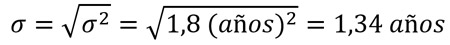
El valor de la desviación estándar poblacional es de 1,34 años.
Guía de ejercicios
A continuación, encontrarás la guía de ejercicios de medidas de dispersión. Resolveremos los ejercicios de varianza y desviación estándar en los videos.
Varianza y desviación estándar, ejercicios propuestos en PDF.
Video
En el siguiente video, veremos una explicación detallada del cálculo de la varianza y desviación estándar a partir de una tabla de frecuencias con variables discretas.
Hasta aquí llegamos por hoy, pero recuerda que aún tenemos muchas clases más de varianza y desviación estándar.


