Propiedad asociativa de la multiplicación
Hoy estudiaremos la propiedad asociativa de la multiplicación con ayuda de muchos ejemplos.
Propiedad asociativa de la multiplicación
"El orden en que se agrupan o asocian los factores, no altera el producto."Ejemplo 1
A continuación, vamos a calcular el valor de 1 × 2 × 6 de dos formas diferentes. La primera forma consiste en agrupar el 1 con el 2 con ayuda de un paréntesis. La segunda forma consiste en agrupar el 2 con el 6. Luego veremos si el producto es el mismo o no.
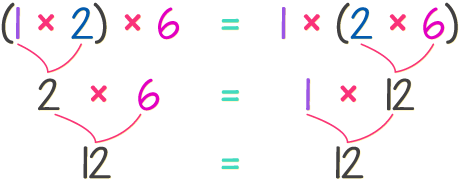
Como puedes ver, aunque cambiemos el orden en que se agrupan los factores, el producto sigue siendo el mismo, 12.
Ejemplo 2
En este ejemplo, vamos a calcular el valor de 4 × 2 × 5 de dos formas distintas. La primera forma consiste en agrupar el 4 con el 2 con ayuda de un paréntesis. La segunda forma consiste en agrupar el 2 con el 5. Después comprobaremos si el producto es el mismo o no.
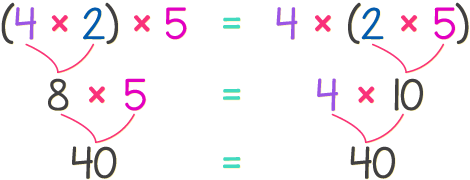
Como puedes ver, aunque cambiemos el orden en que se agrupan los factores, el producto sigue siendo el mismo, 40.
Ejemplo 3
En esta figura tenemos muchas cajas de jugo de manzana y tenemos que calcular el total de cajas.

Para encontrar el total de cajas, vamos a multiplicar el número de estantes (2) por el número de filas en cada estante (3) por el número de cajas en cada estante (4).

A continuación, vamos a calcular el valor de 2 × 3 × 4 de dos formas diferentes. La primera forma consiste en agrupar el 2 con el 3 con ayuda de un paréntesis. La segunda forma consiste en agrupar el 3 con el 4. Luego veremos si el producto es el mismo o no.
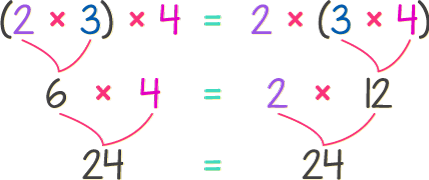
Como puedes ver, aunque cambiemos el orden en que agrupan los factores, el producto sigue siendo el mismo, 24.
Video
En el siguiente video veremos algunos ejemplos interesantes de la propiedad asociativa de la multiplicación.
Referencias
Para realizar esta clase, hemos consultado estos libros:
- Tussy, K., Gustafson, D. y Koenig, D. (2013). Matemáticas básicas (pp. 45-46). Cengage Learning.
- Santillana (2016). Matemática 4° de primaria (p. 26). Santillana Perú.
- McGraw-Hill Education (2017). Math grade 4 (p. 37). McGraw-Hill.


