Suma de vectores: método del triángulo
El método del triángulo es un método que permite hallar la suma o resultante de dos vectores. El método consiste en ubicar los vectores uno a continuación del otro, unidos mediante cabeza y cola. El vector resultante se obtiene uniendo la cola del primero con la cabeza del último.
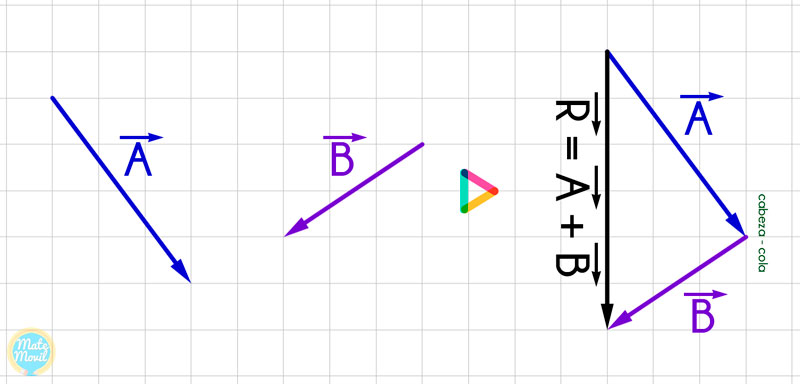
En la siguiente gráfica, vamos a ver como sumar los vectores Ā y B̄ mediante el método del triángulo:

Ejemplo 1:
De manera gráfica, trazar el vector resultante de los vectores Ā y B̄.

Solución:
El vector resultante, es decir, el vector que resulta de sumar los vectores Ā y B̄, lo vamos a obtener mediante el método del triángulo. Por ello, vamos a trasladar los vectores Ā y B̄, de tal manera que los vectores Ā y B̄ se encuentren uno a continuación del otro, unidos mediante cabeza y cola.
El vector resultante, lo veremos de color negro, y se obtiene trazando un vector que parte de la cola del primero y termina en la cabeza del último.
Ejemplo 2:
Para el sistema de vectores mostrado, encontrar el vector resultante:

Solución:
En este ejercicio, tenemos que calcular el vector resultante, es decir, el vector que resulta de sumar los vectores Ā, B̄ y C̄:

En el gráfico, podemos ver que los vectores Ā y B̄, se encuentran uno a continuación del otro, unidos mediante cabeza y cola, por ello, podemos sumarlos usando el método del triángulo. El vector que resulta de sumar el vector Ā y el vector B̄, es el vector que parte de la cola de Ā y termina en la cabeza de B̄, y ese vector, es el vector C̄. Es decir, la suma del vector Ā con el vector B̄, es el vector C̄. Por lo tanto:

Guía de ejercicios
A continuación, viene una guía con muchísimos problemas propuestos de vectores, resolveremos algunos en el video.
Vectores, ejercicios propuestos en PDF
Video
En el siguiente video, veremos diferentes ejercicios del método del triángulo.
Reto

Solución:
Primero encontraremos el vector resultante, es decir, el vector que resulta de sumar los vectores Ā, B̄ y C̄.

En el gráfico, podemos ver que los vectores B̄ y C̄, se encuentran uno a continuación del otro, unidos mediante cabeza y cola, por ello, podemos sumarlos usando el método del triángulo.
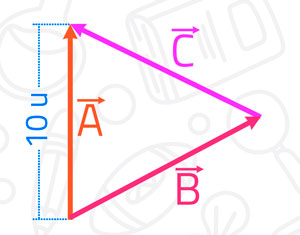
El vector que resulta de sumar el vector B̄ y el vector C̄, es el vector que parte de la cola de B̄ y termina en la cabeza de C̄, y ese vector, es el vector Ā. Es decir, la suma del vector B̄ con el vector C̄, es el vector Ā. Por lo tanto:

Y ahora que ya tenemos el vector resultante, solo nos queda calcular su módulo, es decir, su tamaño o longitud.

Respuesta: 20 u.


