Movimiento parabólico, ejercicios resueltos
El movimiento parabólico de caída libre o MPCL, es un movimiento cuya trayectoria es una curva llamada parábola, en el cual el móvil se mueve únicamente bajo la influencia de la gravedad una vez que es liberado (en vacío, sin aire).
Si un cuerpo se lanza en forma inclinada o se lanza en forma horizontal y se mueve cerca a la tierra despreciando la resistencia del aire, realiza un movimiento parabólico de caída libre, influenciado por la aceleración de la gravedad.

El movimiento parabólico de caída libre es un movimiento compuesto formado por 2 movimientos que se realizan al mismo tiempo y de forma independiente. En el eje horizontal «x» se desarrolla un movimiento rectilíneo uniforme o MRU; mientras que en el eje vertical «y» se desarrolla un movimiento vertical de caída libre o MVCL.

En la mayoría de problemas, tendrás que descomponer el movimiento parabólico en estos 2 movimientos para poder hallar las respuestas. Veamos ahora las fórmulas del movimiento parabólico de caída libre.
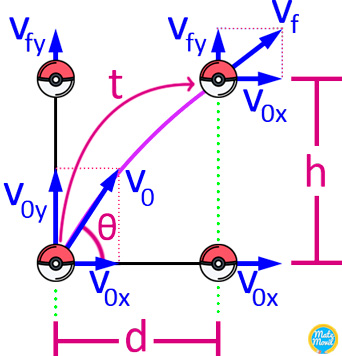
Velocidad inicial

Donde:
- v0 : velocidad inicial.
- v0x : velocidad inicial en el eje x (componente horizontal).
- v0y : velocidad inicial en el eje y (componente vertical).
Eje «x» (Movimiento rectilíneo uniforme – MRU)
Aquí la fórmula con la que trabajaremos será la siguiente:

Donde:
- d : distancia recorrida en el eje «x» o eje horizontal.
- v0x : velocidad inicial en el eje «x».
- t : tiempo del recorrido.

Eje «y» (Movimiento parabólico de caída libre – MPCL)
Mientras que en el eje «y» aplicaremos las siguientes fórmulas de caída libre:

- Usar (+) → si el móvil baja.
- Usar (-) → si el móvil sube.
Donde:
- vfy : velocidad final en el eje «y»
- v0y : velocidad inicial en el eje «y».
- g : aceleración de la gravedad (g = 9,8 m/s2).
- t : tiempo del recorrido.
Fórmulas adicionales
En este capítulo, existen además 4 fórmulas adicionales que nos ahorran mucho tiempo, y son las siguientes:


Siendo:
- Hmax: altura máxima.
- Tvuelo: tiempo de vuelo.
- R: alcance horizontal (espacio recorrido en el eje horizontal x)
- θ: ángulo del vector velocidad inicial con el eje horizontal x.
Antes de iniciar con los problemas, recuerda que el truco consiste en descomponer el movimiento en 2 movimientos: uno en el eje x (MRU) y otro en el eje y (MVCL).
Ejemplo 1:
Desde la parte superior de un edificio de 4,9 metros de altura se lanza horizontalmente una pelota de básquet y cae al suelo en un punto situado a 7 metros del borde del edificio. Hallar la velocidad de la pelota en el instante en que fue lanzada. Usar g = 9,8 m/s2.
Solución:
Primero, realizamos el gráfico de nuestro ejercicio:

Recordamos que el movimiento parabólico de caída libre es un movimiento compuesto, formado por un MVCL en el eje «y» y un MRU en el eje «x». Antes de aplicar las fórmulas, es necesario verificar que trabajamos en el mismo sistema de unidades y en este ejercicio, efectivamente todos los valores se encuentran en el sistema internacional de unidades.
En el eje «y», podemos aplicar la siguiente fórmula, teniendo en cuenta que la velocidad inicial en el eje «y» es cero, ya que la pelota se lanza horizontalmente.
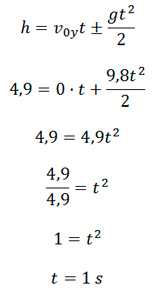
A continuación, en el eje «x», aplicamos la siguiente fórmula:
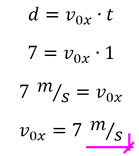
La velocidad inicial en el eje «x» es de 7 m/s.
Guía de ejercicios
Durante los videos resolveremos los ejercicios de la guía que viene a continuación. Hay también más problemas para que puedas practicar en casa:
Movimiento parabólico, problemas propuestos en PDF
Intro
En el siguiente video, veremos un repaso de la teoría del movimiento parabólico y un ejercicio sencillo.
Nivel 1
En el primer nivel, vamos a revisar ejercicios fáciles que nos permitirán saber como usar las fórmulas.
Nivel 2
En el segundo nivel, tenemos 2 problemas de nivel intermedio en los que tendremos que aplicar las propiedades del MPCL.
Nivel 3
Aquí viene el ejercicio resuelto más complicado, y habrá que verlo con calma. Recuerda el truco, descomponer en 2 movimientos, uno en el eje “x” y otro en el eje “y”.
Reto
La esfera mostrada se lanza horizontalmente con v = 20 m/s. Hallar la longitud del plano inclinado.
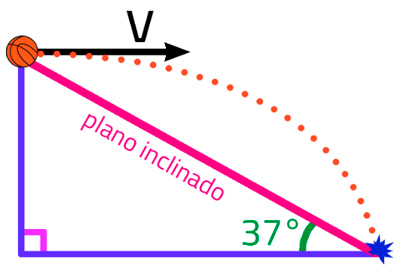
Respuesta: 75 m.


