Movimiento circular uniformemente variado MCUV, ejercicios resueltos
El movimiento circular uniformemente variado o MCUV es un movimiento de trayectoria circular con aceleración angular constante. El MCUV también es llamado movimiento circular uniformemente acelerado (MCUA) o desacelerado. Veamos los detalles y también los ejemplos que hemos preparado.
En este capítulo hay mucha teoría, si te parece difícil, dale un vistazo al video de introducción que encontrarás al final de este artículo.
Por ejemplo, aquí tenemos a nuestra pokebola realizando un movimiento circular uniformemente variado o MCUV, realiza una trayectoria circular con aceleración angular constante. Por ello, a medida que avanza el tiempo, su velocidad cambia de manera constante.

No necesariamente tiene que aumentar la velocidad a medida que pasa el tiempo, también puede que esta disminuya, es decir, que sea un movimiento desacelerado.

Recordemos algunos de los conceptos que aprendimos en el capítulo de movimiento circular uniforme o MCU.
Rapidez angular (ω):
Indica el ángulo que el radio de giro barre por cada unidad de tiempo.
Por ejemplo, si nuestra pokebola realiza un movimiento circular y en un determinado instante tiene una rapidez angular de π rad/s, eso significa que:

Significa que en 1 segundo, el radio de giro va a barrer un ángulo de π rad (o 180°).

La rapidez angular es el módulo de la velocidad angular que veremos a continuación.
Velocidad angular
Nos indica que tan rápido gira el cuerpo y en qué dirección lo hace. El módulo de la velocidad angular, es decir, que tan rápido gira el cuerpo, es la rapidez angular.
Velocidad angular = rapidez angular + dirección.
En el MCUV, a medida que pasa el tiempo cambia la rapidez angular.
Como cambia la rapidez angular, cambia también la velocidad angular, y por ello, aparece la aceleración angular.
Aceleración angular (α)
Es una magnitud vectorial que indica el cambio de la velocidad angular por unidad de tiempo. En el MCUV, la aceleración angular es constante, nunca va a cambiar.
Ecuaciones angulares del MCUV
Son las siguientes:

Donde:
- ω0 : rapidez angular inicial (rad/s).
- ωf : rapidez angular final (rad/s).
- α : aceleración tangencial (rad/s2).
- t : tiempo (s).
- θ : desplazamiento angular (rad).
Acabamos con las variables angulares, a continuación veremos las variables tangenciales.
Rapidez tangencial (v):
Indica la longitud de arco que el objeto recorre por cada unidad de tiempo.
Por ejemplo, si nos dicen que nuestra pokebola en un determinado instante, tiene una rapidez tangencial de 20 m/s, eso significa que:

Este valor nos indica que en 1 segundo, la pokebola va a recorrer una longitud de arco de 20 metros.
La rapidez tangencial es el módulo de la velocidad tangencial.
Velocidad tangencial (v̄)
La velocidad tangencial es una magnitud vectorial, por ello, se define mediante módulo y dirección.
El módulo de la velocidad tangencial «v̄» es la rapidez tangencial «v».
La dirección de la velocidad tangencial «v̄» es tangente a la circunferencia de la trayectoria, es decir, forma 90° con el radio de la circunferencia.

En el MCUV, la rapidez angular cambia, por ello, cambia también la rapidez tangencial. Como cambia la rapidez tangencial (módulo de la velocidad tangencial), aparece la aceleración tangencial.
Aceleración tangencial
Es una magnitud vectorial que indica el cambio de la velocidad tangencial por unidad de tiempo.
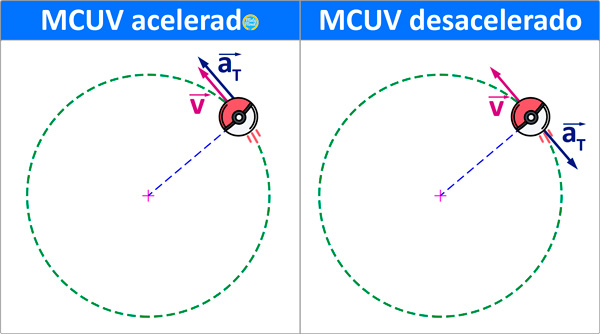
En un movimiento circular acelerado, la aceleración tangencial y la velocidad tangencial apuntan en el mismo sentido. En movimiento desacelerado, la aceleración tangencial y la velocidad tangencial apuntan en sentido opuesto.
Ecuaciones tangenciales
Son las siguientes:

Donde:
- vf : rapidez tangencial final (m/s).
- v0 : rapidez tangencial inicial (m/s).
- at: aceleración tangencial (m/s2).
- t : tiempo (s).
- L : longitud de arco (m).
Aceleraciones
En el MCUV, a medida que pasa el tiempo, cambia la rapidez tangencial, que es el módulo de la velocidad tangencial. Como cambia el módulo de la velocidad tangencial, aparece la aceleración tangencial.
También hay que mencionar que a medida que pasa el tiempo, cambia la dirección de la velocidad tangencial. Como cambia la dirección de la velocidad tangencial, aparece la aceleración centrípeta.

Estas dos aceleraciones, tangencial y centrípeta, al sumarse vectorialmente, dan como resultado la aceleración o aceleración total.

Como la dirección de la aceleración tangencial es perpendicular a la dirección de la aceleración centrípeta, el módulo de la aceleración se calcula así:

Fórmulas auxiliares
Tenemos algunas fórmulas auxiliares que nos permiten relacionar las variables angulares con las variables tangenciales.

Formulario MCUV
Y terminamos con un cuadro con todas las fórmulas que usarás en este capítulo:

Guía de ejercicios
En esta ocasión, hemos preparado una guía con varios ejercicios de MCUV propuestos en PDF, algunos de los cuáles resolveremos juntos en los videos, y los demás, quedarán para que puedas practicar en casa.
Movimiento circular uniformemente variado, ejercicios propuestos
Intro
Veamos un repaso de la teoría y un ejercicio muy sencillo:
Nivel 1
Aquí revisaremos 2 problemas sencillos para ver cómo aplicar las fórmulas del capítulo.
Nivel 2
En el segundo nivel, subimos el nivel y revisaremos 2 problemas interesantes, en los cuáles veremos movimientos acelerados y desacelerados.
Nivel 3
Terminamos con un ejercicio resuelto complicado, en el que tendremos que recordar la suma de vectores.
Reto
Un móvil desarrolla un MCUV, y en un determinado instante, tiene una rapidez tangencial de 120 m/s. Luego de 5 segundos, su rapidez tangencial es de 154 m/s. Si el radio de giro es de 4 m, hallar el módulo de la aceleración angular.
Solución: α = 1,7 rad/s2.


