Distribución normal, ejercicios resueltos
La distribución normal, distribución de Gauss o distribución gaussiana, es la distribución de probabilidad individual más importante. La distribución normal nos permite crear modelos de muchísimas variables y fenómenos, como por ejemplo, la estatura de los habitantes de un país, la temperatura ambiental de una ciudad, los errores de medición y muchos otros fenómenos naturales, sociales y hasta psicológicos. Por ello, hoy vamos a revisar sus características y muchísimos problemas resueltos en 3 niveles de dificultad.
Repaso
¿Qué pasaría si se realiza una encuesta en una ciudad a personas adultas consultando su estatura? A partir de los resultados obtenidos, se puede elaborar un histograma que tendría la siguiente forma:
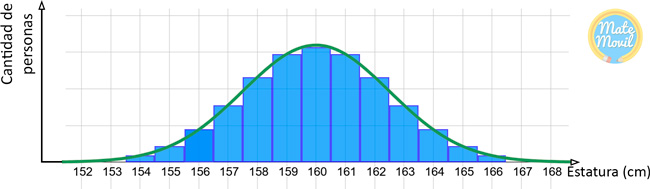
Como vemos, el histograma tiene forma de campana, una característica importante de la distribución normal.
Un parámetro muy importante es la media (µ) y siempre estará al centro de la curva con forma de campana. Por ejemplo, aquí tenemos la gráfica de una distribución normal con media igual a 8.

Además de la media, existe otro parámetro muy importante, se trata de la desviación estándar, representada con la letra griega σ. La desviación estándar es la medida de variabilidad más utilizada y nos indica que tan dispersos se encuentran los datos. Por ejemplo, aquí veremos dos curvas normales, una con desviación estándar pequeña, y otra con desviación estándar grande. Cuando la desviación estándar es pequeña, los datos tienen una dispersión baja y se agrupan alrededor de la media. En cambio, cuando la desviación estándar es alta, los datos tienen una dispersión alta y se alejan de la media.

Características de la distribución normal
Existe una función matemática con forma de campana que tiene la siguiente definición:

Si se grafica esta función, se obtiene como resultado la curva normal:

Además, tiene las siguientes características:
- Toma en cuenta la media(µ) y la desviación estándar(σ).
- El área bajo la curva es igual a 1.
- Es simétrica respecto al centro, o a la media.
- 50% de los valores son mayores que la media, y 50% de los valores son menores que la media.
- La media es igual a la mediana y a la moda.
- Tiene una asíntota en y = 0 (eje x).
Algunos otros ejemplos de variables con distribución normal:
- Notas en un examen.
- Errores de medida.
- Presión sanguínea.
- Tamaño de las piezas producidas por una máquina.
Para encontrar las probabilidades o cantidad de datos entre determinados valores de la variable, se calcula el área bajo la curva normal, que se encuentra en la tabla z o tabla de áreas bajo la curva normal estandarizada.
La distribución normal estándar
La distribución normal estándar, es aquella distribución normal que tiene una media igual a cero, y una desviación estándar igual a uno. Veamos la función densidad normal estandarizada, que trabaja con la variable estandarizada z en el eje horizontal:

Por ejemplo, si se desea encontrar la probabilidad de que la variable estandarizada z, tome un valor entre 0 y 1,50; hay que encontrar el área bajo la curva entre z = 0 y z = 1,50.

Para calcular el valor de esta área, se utiliza la tabla z y se busca el valor de 1,50:
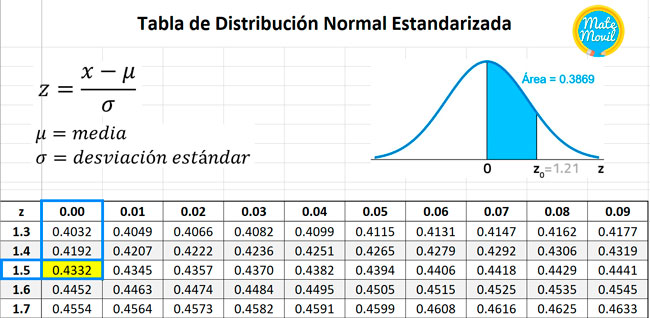
Como vemos, el valor del área bajo la curva es de 0,4332, y esa sería la probabilidad de que la variable estandarizada z, tome un valor comprendido entre 0 y 1,50.
¿Y si mi distribución normal no es estandarizada?
En la mayoría de problemas, cuando se analizan diferentes variables x, la distribución normal no tiene la forma estandarizada, es decir, la media no es cero y la desviación estándar no es uno. En esos casos, se convierten los valores de la variable (x) a z, es decir, se estandarizan los valores de la variable (x).
La fórmula de la variable estandarizada «z», la cual indica cuántas desviaciones estándar se aleja el valor x de la media, es la siguiente:

Y luego, con los valores de z, se utiliza la tabla y se calculan las áreas bajo la curva, porcentajes o probabilidades. En los videos que vienen líneas abajo, encontrarás muchos ejemplos.
Por ejemplo, si tenemos una variable aleatoria continua X con una distribución normal no estandarizada, con media igual a 10 y desviación estándar igual a 1, y el problema pide calcular la probabilidad de que la variable X tome un valor entre 10 y 11,50, hay que estandarizar los valores de la variable X aplicando la fórmula de z:

Ahora, veamos la gráfica de esta distribución normal:

Y usando la tabla z, se calcula el área bajo la curva. Cuando z es igual a 1,50, el área bajo la curva es de 0,4332.

Podemos concluir que la probabilidad de que la variable estandarizada z, tome un valor comprendido entre 10 y 11,50 es de 0,4332.
Descarga la tabla z
Desde el siguiente enlace podrás acceder a la tabla de áreas bajo la curva normal. Recuerda imprimirla y llevarla a tu examen.
Tabla z distribución normal estandarizada – MateMovil
Descarga la guía de ejercicios
Además, hemos preparado una guía con varios ejercicios propuestos de distribución normal.
Distribución Normal Ejercicios Propuestos PDF
Nivel 1
En el primer nivel, vamos a revisar las características de la distribución normal y luego resolveremos algunos problemas interesantes con ayuda de la tabla z:
Nivel 2
En este nivel, vamos a resolver varios problemas de nivel intermedio. Además, veremos como resolver problemas de distribución normal al instante usando un simulador o una calculadora.
Nivel 3
Viene ahora el nivel 3, en el que vamos a combinar ejercicios de distribución normal con otros temas matemáticos:
Reto
Antes de ir a tu examen, puedes practicar con estos ejercicios. Encontrarás la solución líneas abajo:
6. Los sueldos mensuales en una empresa siguen una distribución normal con media de 1200 soles, y desviación estándar de 200 soles. ¿Qué porcentaje de trabajadores ganan entre 1000 y 1550 soles?
7. Una fábrica de producción de agua embotellada, cuenta con una máquina de envasado automático, la cual vierte en cada botella una cierta cantidad de agua que sigue una distribución normal con media de 500 mililitros y una varianza de 25 mililitros. ¿Qué porcentaje de las botellas se llenan con agua entre 490 y 507 mililitros?
Solución
Descarga la solución de ambos problemas desde aquí:
Distribución Normal Ejercicios Resueltos PDF
¿Quieres aprender un poco más?
Te dejo por aquí un artículo de distribución normal que está muy interesante.


