Variables aleatorias discretas y continuas
Una variable aleatoria es una función que asigna un valor numérico, al resultado de un experimento aleatorio. Una variable aleatoria puede ser discreta o continua. Las variables aleatorias discretas son aquellas que presentan un número contable de valores; por ejemplo, el número de personas que viven en una casa (pueden ser 3, 5 o 9). Las variables aleatorias continuas son aquellas que presentan un número incontable de valores; por ejemplo, el peso de las vacas en una granja (una vaca puede pesar 632,12 kg, otra puede pesar 583,12312 kg, otra 253,12012 kg, otra 198,0876 kg y nunca terminaríamos de enumerar todos los posibles valores).
Como estas definiciones son muy difíciles de entender a simple vista, vamos a explicarlas a detalle.
Contenido
- Variable aleatoria.
- Variable aleatoria discreta.
- Variable aleatoria continua.
- Guía de ejercicios.
- Video.
- Reto.
Variable aleatoria
Una variable aleatoria es una función que asigna un valor numérico, al resultado de un experimento aleatorio. Recordemos que el resultado de un experimento aleatorio depende del azar. Veamos los ejemplos.
Ejemplo 1 de variable aleatoria
Tenemos una moneda que en sus caras tiene por un lado un gato y por el otro, un perro.

Vamos a realizar un experimento aleatorio que consiste en lanzar 2 monedas. Colocaremos los resultados en el siguiente gráfico:

Definimos nuestra variable aleatoria X:
- X = número de perros.
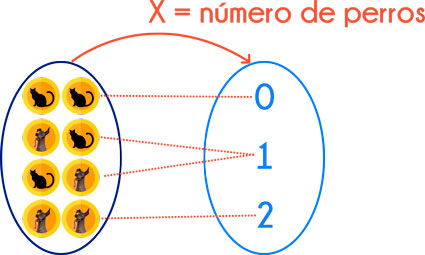
Ten en cuenta que la variable aleatoria siempre va con letras mayúsculas (en este caso X), mientras que los valores de su rango siempre con letras minúsculas (en este caso x1 , x2 , x3).
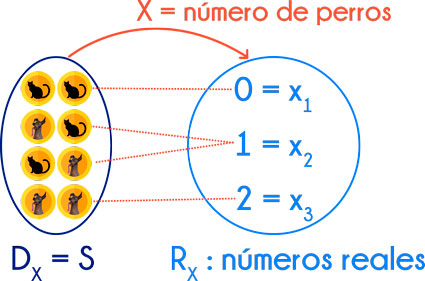
Los valores del rango de esta variable aleatoria son:
- x1 = 0
- x2 = 1
- x3 = 2
En el dominio de la función tenemos el espacio muestral, es decir, todos los resultados posibles de nuestro experimento aleatorio. Mientras que el rango tenemos un conjunto de números reales.
Ejemplo 2 de variable aleatoria
En un banco hay 3 cajeros automáticos. Vamos a realizar un experimento aleatorio que consiste en ir al banco a una hora al azar del día y ver qué cajeros están ocupados y qué cajeros están vacíos.
Colocamos en el siguiente gráfico los resultados, los cajeros vacíos (V) irán de color rojo y los ocupados (O) de color verde.

Definimos nuestra variable aleatoria Y:
- Y = número de cajeros automáticos ocupados.

Ten en cuenta que la variable aleatoria siempre va con letras mayúsculas (en este caso Y), mientras que los valores de su rango siempre con letras minúsculas (en este caso y1 , y2 , y3, y4).

Los valores del rango de esta variable aleatoria son:
- y1 = 0
- y2 = 1
- y3 = 2
- y4 = 3
Las variables aleatorias se clasifican en discretas o continuas en función de los valores numéricos que asumen. Veamos esto a detalle.
Variable aleatoria discreta
Una variable aleatoria discreta es aquella que puede asumir un número contable de valores. Por ejemplo, si realizamos el experimento de salir a calle y seleccionar 10 personas al azar para un examen sorpresa de matemáticas, podemos definir la variable aleatoria A:
- A = número de personas que aprobaron el examen.
Los valores que asume A (en su rango), van del 0 al 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10). El rango lo expresaríamos de la siguiente manera:
- RA = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
La variable aleatoria A asume un número contable de valores, por ello, es una variable aleatoria discreta.
Otro ejemplo, vamos a realizar el experimento de registrar los automóviles a una caseta de peaje. Podemos definir la variable aleatoria V:
- V = número de vehículos que llegan durante el periodo de un día.
Los valores que asume V (en su rango), son 0, 1, 2, 3, 4, 5, …; así sean muchos vehículos los que llegan, siempre podremos contar la cantidad de valores que asume V. Por ello, la variable V es una variable aleatoria discreta.
Variable aleatoria continua
Una variable aleatoria continua, es aquella que puede asumir un número incontable de valores.Por ejemplo, si realizamos el experimento de ir a mi granja y estudiamos las características de las vaquitas, podemos definir la variable aleatoria C:
- B = peso de una vaca en la granja de Jorge (en kilogramos).
Alguna vaquita puede pesar 425,1872 kg; otra puede pesar 612,5874541 kg; otra puede pesar 545,897512121 kg. Si tomamos más vacas, podríamos tener más valores y nunca terminaríamos.
Se conoce que el becerro más pequeño tiene un peso de 30 kg, y la vaca más grande tiene un peso de 1000 kg.

Y así, tendríamos un número incontable de valores para el rango de esta variable. El rango de esta variable puede ser cualquier valor dentro del intervalo que va desde 30 kg hasta 1000 kg.
Por ello, se trata de una variable aleatoria continua.
Otro ejemplo, si vamos a una agencia del banco y registramos los datos de atención a los clientes, podemos definir la variable aleatoria D:
- D = tiempo de atención a los clientes del banco (en segundos).
Un cliente puede ser atentido en 24,123 s; otro cliente en 72,32142 s; otro en 51,123123 s. Si seguimos tomando más clientes, tendríamos más valores. Se conoce además que el tiempo mínimo de atención en ventanilla es de 1 s y el tiempo máximo es de 240 s.

Y así, tendríamos un número incontable de valores para el rango de esta variable. El rango de esta variable puede ser cualquier valor dentro del intervalo que va desde 1 s hasta 240 s. Por ello, se trata de una variable aleatoria continua.
En general, las variables aleatorias discretas representan datos que provienen del conteo del número de elementos, mientras que, las variables aleatorias continuas representan datos que provienen de mediciones, por ejemplo, tiempo, peso, longitud, etc.
Guía de ejercicios
A continuación, viene una guía de ejercicios en PDF. Resolveremos algunos de los ejercicios en los videos.
Video
En el siguiente video, repasaremos los conceptos de variable aleatoria y también veremos ejemplos de variables aleatorias discretas y continuas.
Video 2
En este segundo video, vamos a resolver ejercicios en los que tenemos que diferenciar a las variables aleatorias discretas de las variables aleatorias continuas.
Reto
Se realiza una encuesta en un salón acerca de la estatura de los alumnos y el número de hermanos que tienen. Identifica las 2 variables aleatorias de interés, sus posibles valores e indica si son discretas o continuas.
Respuesta:
- A = estatura de los alumnos. Variable aleatoria continua. La estatura se relaciona a la medición y puede asumir un número incontable de valores.
- B = número de hermanos de los alumnos. Variable aleatoria discreta. Esta variable aleatoria se relaciona al conteo, ya que hay que hay que contar el número de hermanos, y puede asumir un número contable de valores.
Hasta aquí llegamos por hoy, pero recuerda que en las siguientes clases combinaremos con las variables aleatorias con probabilidades.


