Teorema de la probabilidad total
El teorema de la probabilidad total permite calcular la probabilidad de que ocurra un evento, que se puede realizar a través de varios caminos. Antes de revisar el teorema de probabilidad total, es necesario definir el concepto de «partición».
Veamos los ejemplos y ejercicios del teorema de la probabilidad total.
Partición
Sean A1, A2, A2, … , An, eventos de un mismo espacio muestral S. Dichos eventos forman una partición de S si son mutuamente excluyentes y colectivamente exhaustivos. Es decir, si cumplen con las condiciones siguientes:

Teorema de la probabilidad total
El teorema de la probabilidad total, establece que:
Sean A1, A2, A3, … , An, eventos que forman una partición del espacio muestral S, y sea B otro evento cualquiera del espacio muestral S, entonces la probabilidad del evento B se puede obtener de la siguiente manera:

Los problemas de probabilidades que requieren al teorema de probabilidad total, también se pueden resolver de manera sencilla usando el diagrama de árbol. Vamos a revisar 1 ejercicio, y lo vamos a resolver con el diagrama de árbol y con el teorema.
Ejercicio 1:
En un acuario se tienen solo 2 especies de peces, el 40% son de la especie azul y el 60% son de la especie roja. De la especie azul, el 30% son machos; mientras que, de la especie roja, el 40% son hembras. ¿Cuál es la probabilidad de que un pez elegido aleatoriamente en el acuario sea macho?
Solución con el diagrama de árbol:
A partir de los datos del enunciado, vamos a elaborar el diagrama de árbol.

Recuerda el truco que usamos para calcular probabilidades usando el diagrama de árbol: cuando avanzamos de izquierda a derecha, multiplicamos las probabilidades; cuando avanzamos de arriba hacia abajo, sumamos las probabilidades.

La probabilidad de encontrar un macho, seleccionando un pez de forma aleatoria es de 0,48 o 48%.
Solución con el teorema de probabilidad total:
Ahora resolvemos el mismo problema usando el teorema. Tenemos 2 eventos A1 y A2, que forman una partición del espacio muestral S (peces del acuario):
- A1: que un pez elegido aleatoriamente sea de la especie azul.
- A2: que un pez elegido aleatoriamente sea de la especie roja.

A partir del gráfico, sabemos que:
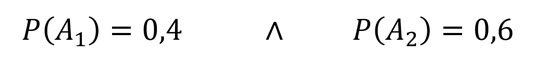
También tenemos al evento B:
- B: que un pez elegido aleatoriamente sea macho.
Nos dicen que de la especie azul, el 30% son machos. Por ello, sabemos que la probabilidad de que un pez sea macho, dado que es de la especie azul, es de:
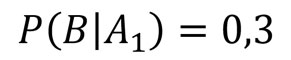
Nos dicen que el 40% de los peces de la especia roja son hembras, por ello, el 60% serán machos. Entonces, sabemos que la probabilidad de que un pez sea macho, dado que es de la especie roja:

Recordemos el teorema de probabilidad total:

En nuestro caso, tenemos una partición del espacio muestral S, formada solo por 2 eventos: A1 y A2 .

Reemplazando nuestros valores:

La probabilidad de que un pez elegido aleatoriamente sea macho, es de 0,48 o 48 %.
Guía de ejercicios
A continuación, viene una guía con muchos ejercicios de probabilidades en PDF.
Probabilidades, ejercicios propuestos PDF
Video
En el siguiente video, vamos a resolver algunos ejercicios mediante el diagrama de árbol, el teorema de la probabilidad total y también realizaremos la demostración del mismo.
Hasta aquí llegamos por hoy, continuamos en las siguientes clases del curso de estadística.


