Media o valor esperado, varianza y desviación estándar de una variable aleatoria continua
El día de hoy veremos cómo calcular la media (esperanza o valor esperado), la varianza y la desviación estándar de una variable aleatoria continua a partir de su función de densidad de probabilidad.
Para las fórmulas que veremos a continuación, trabajaremos con la variable aleatoria continua X con función de densidad de probabilidad f(x).
1. Media o valor esperado
La media, llamada también valor esperado o esperanza, se denota con μ o E(X) y su fórmula es:
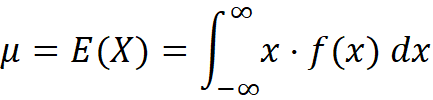
2. Varianza
Es una medida de dispersión, se representa con σ2 o V(X) y su fórmula es:

Una fórmula alternativa y mucho más rápida es la siguiente:

3. Desviación estándar
Es una medida de dispersión. Se representa con σ y se calcula teniendo en cuenta que es la raíz cuadrada (positiva) de la varianza:

La varianza y la desviación estándar dan medidas cuantitativas de cuánta dispersión hay en la distribución o población de valores x.
4. Ejemplo 1
La variable aleatoria continua X tiene la siguiente función de densidad de probabilidad:

Calcular el valor esperado, la varianza y la desviación estándar.
Solución:
Empezaremos graficando esta función de densidad de probabilidad. Yo lo haré con ayuda de GeoGebra, pero puedes hacerlo manualmente.

Ten en cuenta que la función de densidad obtenida, tiene 3 tramos.
Ahora sí, calculamos la media o valor esperado:
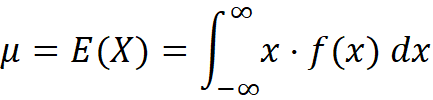
Como la función tiene 3 tramos, expresaremos la integral original como la suma de 3 integrales:







Luego, calcularemos la varianza. Es mejor usar la fórmula alternativa:











Terminamos con la desviación estándar, que es la raíz cuadrada positiva de la varianza:


5. Guía de ejercicios
A continuación, podrás descargar la guía de ejercicios.
6. Video
A continuación, viene un ejercicio muy interesante de media o valor esperado, varianza y desviación estándar.
7. Referencias
- Devore, J. (2016). Probabilidad y estadística para ingeniería y ciencias. 9a ed. Ciudad de México: Cengage Learning, pp.148-150.
- Córdova Zamora, M. (2009). Estadística Descriptiva E Inferencial. 5th ed. Lima: Moshera, p.212.
- Montgomery, D. and Runger, G. (2014). Applied Statistics And Probability For Engineers. 6th ed. USA, pp.114-115.
- Navidi, W. (2006). Estadística para ingenieros. 1a ed. México: McGraw-Hill, pp.101-105.


