Función de distribución acumulativa de una variable aleatoria discreta
La función de distribución acumulativa especifica la probabilidad de que una variable aleatoria sea menor o igual a un valor dado. La función de distribución acumulativa de la variable aleatoria X es la función F(x) = P(X ≤ x). Para que se entienda mejor, vamos a revisar algunos ejemplos y ejercicios.
Antes de empezar, un pequeño consejo, no hay que confundir la función de probabilidad con la función de distribución acumulativa.
1. Introducción
La función de probabilidad de una variable aleatoria discreta que estudiamos en un capítulo anterior, nos indica la probabilidad de que la variable aleatoria sea igual a un valor determinado. Pero la función de distribución acumulativa especifica la probabilidad de que una variable aleatoria sea menor o igual que un valor dado. A la función de distribución acumulativa la denominamos F(x) y su fórmula es la siguiente:

Vamos a mencionar 2 propiedades importantes:
- Los valores de F(x) se encuentran siempre en este intervalo: 0 ≤ F(x) ≤ 1.
- F(x) no es una función decreciente.
Además, para la función de distribución acumulativa de la variable aleatoria discreta, se cumple que:

2. Ejemplos
Ejemplo 1:
Una tienda vende discos duros de 1 TB, 2 TB y 3 TB de capacidad. Encontrar la función de distribución de acumulativa de X, sabiendo que X = la capacidad de memoria en un disco duro comprado:

Solución:
Nos piden encontrar la función de distribución acumulativa de X, entonces recordemos la fórmula:

Primero vamos a encontrar F(x) para cada uno de los posibles valores de X:

Completamos la tabla:
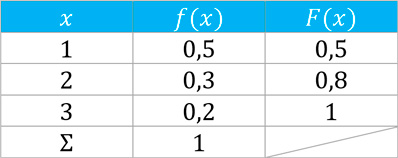
Vamos a borrar la columna f(x) para no generar confusión:

A continuación, elaboramos la gráfica de x vs F(x):

En la gráfica, colocamos líneas continuas entre los valores, partiendo desde el lado izquierdo:

Y listo, solo nos queda definir la función F(x) a partir de la gráfica:

Además, pudimos comprobar que los valores de F(x) se encuentran entre 0 y 1, y también, que F(x) no es una función decreciente. Estas son 2 propiedades importantes de la función de probabilidad.
Ejemplo 2:
Una moneda tiene en sus caras, un gato y un perro. Encontrar la función de distribución acumulativa del número de perros obtenidos al lanzar 2 monedas y graficar la función.

Solución:
Arrancamos definiendo la variable aleatoria discreta con la que vamos a trabajar:
- X = número de perros obtenidos al lanzar 2 monedas.
Si lanzamos dos monedas, podemos obtener los siguientes resultados: gato con gato, gato con perro, perro con gato o por último, perro con perro.
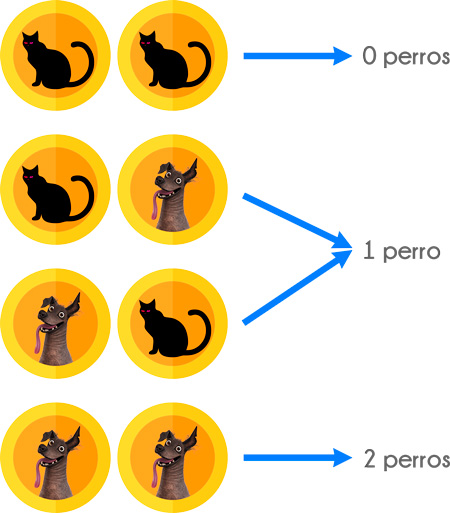
A continuación, colocamos en una tablita vertical, los valores de la variable aleatoria X (número de perros obtenidos al lanzar 2 monedas):
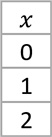
A cada valor de la variable aleatoria, le asignamos una probabilidad:

Y completamos la tablita que venimos construyendo, agregando la columna de la función de probabilidad:

Ahora sí, vamos con la función de distribución acumulativa, recordando su fórmula:

i) Calculamos los valores de F(x), empezando con F(0).

La probabilidad de obtener 0 perros o menos al lanzar 2 monedas, es 0,25.
ii) Continuamos con F(1):

La probabilidad de obtener 1 perro o menos al lanzar 2 monedas, es 0,75.
iii) Seguimos con F(2):
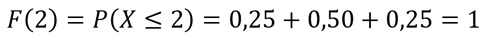
La probabilidad de obtener 2 perros o menos al lanzar 2 monedas, es 1.
Completamos nuestra tablita:

Puedes ver en la tabla como los valores de f(x) se van acumulando para obtener los valores de F(x).
Agradecemos a f(x) por su participación, pero ya no la necesitamos. Nos quedamos con x y F(x):

Y empezamos nuestra gráfica de F(x), marcando los puntos de la tabla:

En la gráfica, colocamos líneas continuas entre los valores, partiendo desde el lado izquierdo:

Y ahora sí, solo nos queda pasar la información de la gráfica a la definición de F(x):

Ejemplo 3:
Sea X el número de defectos importantes en un auto seleccionado al azar de cierta marca. La función de distribución acumulativa de X es la siguiente:
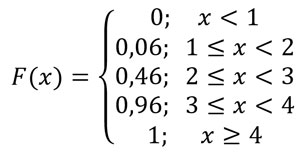
Calcule las siguientes probabilidades:
a) f (2)
b) P (X≤ 3)
c) P (1 < X ≤ 3)
d) P (1 < X ≤ 4)
e) P (X ≥ 2,35)
Solución:
A partir de la función de distribución acumulativa, vamos a elaborar la tabla de la función de probabilidad. Empezamos colocando una tabla de 3 columnas. Los valores de X los obtenemos de los extremos de los intervalos que aparecen en la función de distribución acumulativa. No tomes en cuenta la primera línea de la función de distribución acumulativa.

A continuación, encontraremos los valores de f(x) a partir de los valores de la función de distribución acumulativa F(x). Esto se parece mucho a lo que hicimos en el capítulo de tablas de frecuencia. Arrancamos colocando el primer valor de F(x) en la columna de f(x).

Después calculamos el resto de valores, ten en cuenta que los valores de f(x) se van acumulando para dar paso a los valores de F(x) y los agregamos a la tabla:

Calculamos lo que pide el problema:
a) f(2)
Lo obtenemos a partir de la tabla:
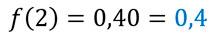
b) P(X ≤ 3)
Partimos de la fórmula de la función de distribución acumulativa, reemplazando x por 3.
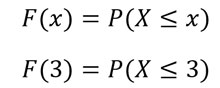
Le damos la vuelta a la ecuación:
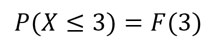
A partir de la tabla:
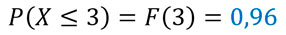
c) P(1 < X ≤ 3)
En este apartado, usaremos la siguiente propiedad:
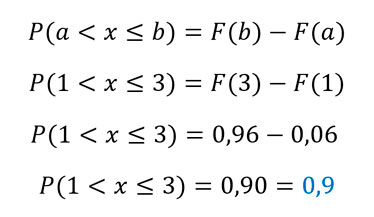
d) P(1 < X ≤ 4)
Usamos la misma propiedad:
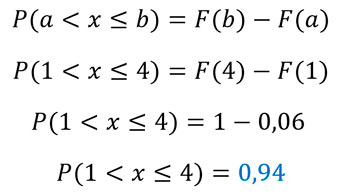
e) P(X ≥ 2,35)
A partir de la tabla, sabemos que la variable aleatoria X puede tomar los valores: 1, 2, 3 o 4. Si X tiene que ser mayor a 2,35; puede ser 3 o 4.

3. Guía de ejercicios
A continuación, viene una guía con muchos ejercicios de variables aleatorias, resolveremos algunos en los videos.
4. Videos
Como siempre, hemos preparado algunos videos con todo lo que debes saber de la función de distribución acumulativa.
Empezamos con el video de teoría:
Y continuamos con un ejercicio:
Hasta aquí llegamos por hoy, recuerda que tenemos muchísimas otras clases del curso de estadística.
5. Referencias
- Navidi, W. (2006). Estadística para ingenieros. 1a ed. México: McGraw-Hill, p.92.
- Johnson, R. (2012). Probabilidad y estadística para ingenieros, Miller y Freund. 8a ed. Estado de México: Pearson, p.84.
- Wisniewski, P. (2014). Estadística y probabilidad. 1ra ed. México: Editorial Trillas, p.114.


