Permutaciones y combinaciones, ejercicios resueltos
Una permutación de un conjunto de elementos, es una disposición de dichos elementos teniendo en cuenta el orden. Una combinación de un conjunto de elementos, es una selección de dichos elementos sin tener en cuenta el orden.
La diferencia entre permutaciones y combinaciones, es que en las permutaciones importa el orden de los elementos, mientras que en las combinaciones no importa el orden en que se disponen los elementos (solo importa su presencia).
Veamos algunos conceptos adicionales, ejemplos y ejercicios resueltos.
Permutaciones
Una permutación de un conjunto de elementos, es una disposición de dichos elementos teniendo en cuenta el orden. El número de permutaciones de “n” elementos tomados de “k” en “k” se calcula con la fórmula:
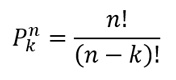
Ejemplo 1:
Eduardo, Carlos y Sergio se han presentado a un concurso de pintura. El concurso otorga $200 al primer lugar y $100 al segundo. ¿De cuántas formas se pueden repartir los premios de primer y segundo lugar?
Solución:
En este caso, si importa el orden, ya que no es lo mismo quedar en primer lugar que en segundo, además, los premios son diferentes. Por ejemplo, un arreglo o disposición, es que Carlos ocupe el primer lugar y Sergio el segundo. Otro arreglo, sería que Sergio ocupe el primer lugar y Eduardo el segundo. El número total de arreglos o formas lo calculamos con la fórmula:

Combinaciones
Una combinación de un conjunto de elementos, es una selección de dichos elementos sin tener en cuenta el orden.
El número de combinaciones de “n” elementos tomados de “k” en “k” se calcula con la fórmula:

Ejemplo 2:
Un chef va a preparar una ensalada de verduras con tomate, zanahoria, papa y brócoli. ¿De cuántas formas se puede preparar la ensalada usando solo 2 ingredientes?
Solución:
En este caso, no importa el orden en que se tomen los ingredientes para la ensalada, pues da igual si es una ensalada de tomate con zanahoria, que una ensalada de zanahoria con tomate, ya que al final, el chef mezclará los dos ingredientes.
Un arreglo podría ser zanahoria y tomate, otro arreglo podría ser tomate y papa, otro arreglo podría ser papa y brócoli. El problema nos indica que solo se pueden usar 2 ingredientes en la ensalada. El número total de arreglos o formas lo calculamos con la fórmula:

Ejemplo 3:
Se va a programar un torneo de ajedrez para los 10 integrantes de un club. ¿Cuántos partidos se deben programar si cada integrante jugará con cada uno de los demás sin partidos de revancha?
Solución:
En este torneo se van a realizar partidas de ajedrez en cada una de las cuales participan 2 jugadores. Por ello, necesitamos ordenamientos de 2 en 2, es decir, k = 2. Además, en estos ordenamientos participarán los 10 jugadores, por eso, n = 10.
En este caso, no importa el orden, ya que solo necesitamos agrupar los jugadores, es igual que juegue Jorge contra Carlos, que Carlos contra Jorge. Además, no hay partido de revancha, es una sola partida con cada contrincante.

Se deben programar 45 partidos.
Ejemplo 4:
Considera un grupo de 10 estudiantes de los cuales 4 son mujeres y 6 son hombres. De acuerdo con esa información, determine:
a) El número de formas en que se puede elegir un representante del grupo .
b) El número de formas en que se puede elegir un comité de 3 miembros, donde al menos uno de los miembros sea mujer.
Solución:
En este caso, no nos dicen que el comité tiene rangos, por lo tanto, no importa el orden. Aplicaremos la fórmula de combinaciones.
a) El número de formas en que se puede elegir un representante del grupo .
De un total de 10 miembros, elegiremos a uno:

b) El número de formas en que se puede elegir un comité de 3 miembros, donde al menos uno de los miembros sea mujer.
Al menos uno de los 3 miembros tiene que ser mujer. Eso significa que el comité puede estar formado por 1, 2 o 3 mujeres.
– Si el comité está formato por 1 mujer, significa que de las 4 mujeres seleccionaremos una, y de los 6 hombres seleccionaremos 2.

– Si el comité está formato por 2 mujer, significa que de las 4 mujeres seleccionaremos 2, y de los 6 hombres seleccionaremos 1.

– Si el comité está formato por 3 mujeres, significa que de las 4 mujeres seleccionaremos 3, y de los 6 hombres no seleccionaremos a ninguno.

En total, tenemos:

Guía de ejercicios
A continuación, viene una guía de ejercicios en PDF que iremos resolviendo juntos en los videos.
Permutaciones y combinaciones, ejercicios resueltos en PDF
Nivel 1
En el primer nivel, vamos a realizar un repaso de los conceptos de permutaciones y combinaciones, y resolveremos algunos problemas sencillos.
Nivel 2A
En este segundo nivel, vamos a resolver 2 problemas adicionales. Uno de permutaciones, y otro de combinaciones.
Nivel 2B
Veamos ahora un clásico ejercicio de permutaciones. Tiene varios apartados, y los apartados del final son muy complicados:
Nivel 3
Viene ahora un problema interesante, en el que vamos a combinar las permutaciones y combinaciones con el principio de adición y el principio de multiplicación.
Permutación con repetición
Cuando existen elementos repetidos, las reglas de juego y la fórmula cambia:
Permutación circular
Si los elementos se ordenan en círculo, entonces, la fórmula cambia. Veamos de que se trata:
Reto
Con 4 frutas diferentes, ¿cuántos jugos surtidos se pueden preparar? Un jugo surtido se prepara con 2 frutas al menos.
Solución:
Los jugos se pueden preparar con 2 frutas, con 3 frutas o con 4 frutas:
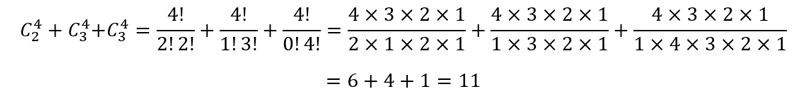
En total, se pueden preparar 11 jugos surtidos.


