Resta de fracciones con diferente denominador (fracciones heterogéneas)
En la clase de hoy veremos cómo restar fracciones con diferente denominador (fracciones heterogéneas) con ayuda de varios ejemplos.
Contenido:
- Método 1: resta rápida.
- Ejemplo 1.
- Ejemplo 2.
- Ejemplo 3.
- Ejemplo 4.
- Método 2: usando el MCM.
- Ejemplo 5.
- Ejemplo 6.
- Videos.
- Referencias.
Método 1: resta rápida
Para restar rápidamente 2 fracciones, usaremos esta regla:

Primero multiplicamos los denominadores (b×d), después multiplicamos en aspa y restamos esos productos cómo se ve en la figura. Es bien fácil, ya lo verás en los ejemplos.
1) Calcular 1⁄2 – 1⁄3:
Estas fracciones tienen distinto denominador, por eso, para realizar la resta aplicamos nuestra regla:

La respuesta es 1⁄6.
2) Calcular 3⁄4 – 2⁄5:
Estas fracciones tienen diferentes denominadores, por eso, para realizar la resta, primero multiplicamos los denominadores y luego viene la multiplicación en aspa.

3) Calcular 1⁄2 – 1⁄4:
Estas fracciones tienen distinto denominador, por eso, para realizar la resta, primero multiplicamos los denominadores y después realizamos la multiplicación en aspa. Aquí veremos la solución:

Luego de realizar los pasos, se obtiene 2⁄8, pero esta es una fracción que se puede simplificar. Luego de simplificar, la respuesta final es 1⁄4.
4) Calcular 5⁄6 – 2⁄3:
Estas fracciones tienen diferentes denominadores, entonces, aplicamos la regla para restar fracciones:

Luego de operar, se obtiene como resultado 3⁄18, esta fracción se puede simplificar dividiendo el numerador y el denominador entre 3. Luego de simplificar, se obtiene 1⁄6 como respuesta final.
Método 2: usando el MCM
Para restar fracciones con el mismo denominador, buscamos el mínimo común múltiplo (MCM) de los denominadores, conocido también como mínimo común denominador, éste lo dividimos entre cada uno de los denominadores de las fracciones y los resultados los multiplicamos por su correspondiente numerador. Al final, restamos los números para llegar al resultado final. Suena complicado, pero se entenderá con algunos ejemplos.
5) Calcular 1⁄2 – 1⁄3:
Primero se calcula el mínimo común múltiplo (MCM) de los denominadores (6) y luego vienen el resto de pasos:
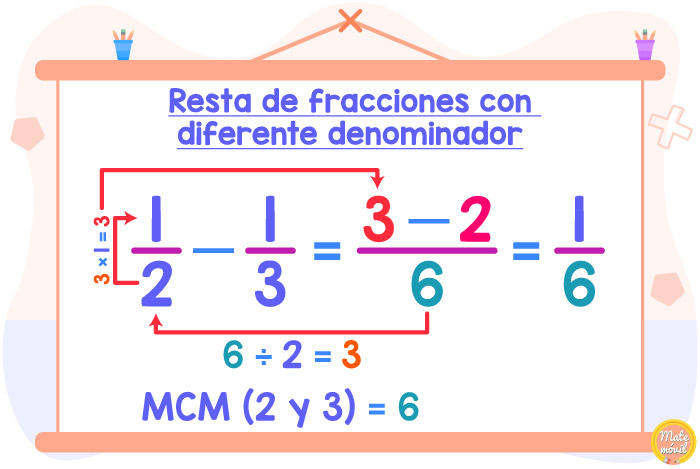
6) Calcular 3⁄4 – 2⁄5:
Iniciamos calculando el mínimo común múltiplo (MCM) de los denominadores o mínimo común denominador (20). Después vienen el resto de pasos:

Videos
En este video, veremos algunos ejemplos muy sencillos de resta de fracciones con distinto denominador:
A continuación, vienen 2 ejercicios muy sencillos:
Y terminamos con algunos ejercicios más de resta de fracciones heterogéneas:
Referencias:
- Fandiño, M. (2009). Las fracciones: aspectos conceptuales y didácticos (p. 146).
- CONAMAT (2009). Matemáticas simplificadas (pp. 53-54). Prentice Hall.


