Límites infinitos, ejercicios resueltos
Los límites infinitos son aquellos en los que las imágenes f(x) aumentan o disminuyen sin límite cuando x se aproxima a un valor a. Existen varios casos de límites infinitos, veamos algunos ejemplos, ejercicios resueltos y aplicaciones.
De forma general, los representamos como:
![]()
Ejemplo de límite infinito
Indicar si existe el siguiente límite:

Si graficamos la función:

Y si realizamos una tabla de valores:

Para que el límite exista, las imágenes deben acercarse a un valor real cuando las x se acercan a cero. Sin embargo, en este problema, las imágenes no se acercan a ningún valor real. A partir de la gráfica, podemos ver que cuando los valores de x se acercan a cero, las imágenes crecen sin límite, por lo tanto, el límite no existe:

¿Y ahora qué hacemos?
Si bien el límite no existe, podemos usar la notación de límites para expresar el comportamiento de la función: las imágenes tienden a infinito (crecen sin límite) , cuando x tiende a cero.

Eso no quiere decir que el límite exista. Es más, ese infinito es la razón de inexistencia del límite, pues el infinito no es un número real, y para que el límite exista, las imágenes f(x) deben acercarse a un número real.
Otro ejemplo
Tomando en cuenta la gráfica, determinar los siguientes límites laterales:
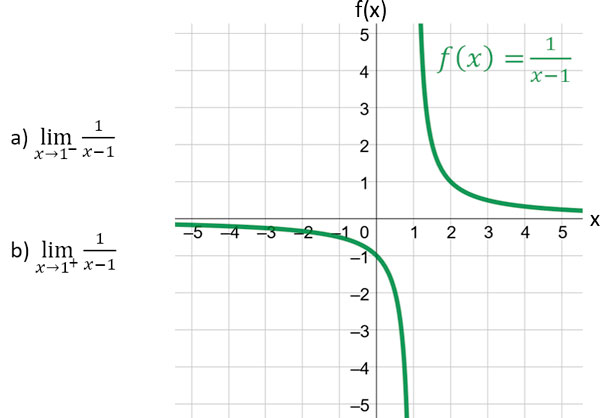
De la gráfica, podemos apreciar que:

Todos los casos de límites infinitos
Dado que los límites infinitos también aparecen en los límites laterales, tenemos varios casos de límites infinitos:

Asíntotas verticales
En todos los casos de límites infinitos, aparece siempre una asíntota vertical en x = a. No lo olvides, siempre que aparece un límite infinito, aparece una asíntota vertical. Ejemplo:

Guía de ejercicios
Desde el siguiente enlace, podrás descargar la guía de ejercicios. Resolveremos algunos problemas en los videos.
Límites infinitos ejercicios propuestos PDF
Videos
A continuación, vienen dos videos de límites infinitos. En el primero veremos un repaso de la teoría y algunos ejercicios. En el segundo viene un problema de aplicación.
Ahora vamos a revisar un problema de aplicación de los límites infinitos. Este problema parece muy complicado, ¿lo será?
Si deseas acceder a la gráfica del problema en GeoGebra, puedes hacerlo desde aquí:
Reto
Y para terminar, viene un pequeño reto. La solución va líneas abajo.

Solución:
Usaremos el método de tabla de valores.

Podemos ver que cuando nos acercamos a -1 por la izquierda, los valores de las imágenes f(x) decrecen sin límite. Mientras que si nos acercamos a -1 por la derecha, los valores de las imágenes f(x) crecen sin límite. Por lo tanto:

c) Además, dado que aparece un límite infinito, hay una asíntota vertical en x = -1.


