Función par e impar, simetrías y paridad, ejercicios resueltos
Las funciones pueden clasificarse de acuerdo a su paridad en 3 tipos: funciones pares, funciones impares, y funciones que no tienen paridad. Veamos un pequeño repaso sobre simetrías y paridad.
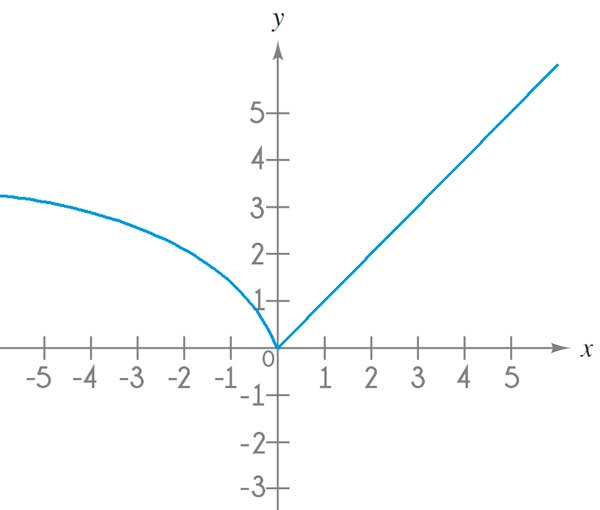
Función par: es aquella que satisface la condición: f(x) = f(-x). De manera gráfica, se caracterizan por ser simétricas respecto al eje y. Veamos un ejemplo:

Función impar: es aquella que satisface la condición: f(x) = -f(-x). De manera gráfica, se caracterizan por ser simétrica respecto al origen. Esta simetría se puede identificar rotando la gráfica 180 grados, y si queda igual que al inicio, entonces es una función impar.
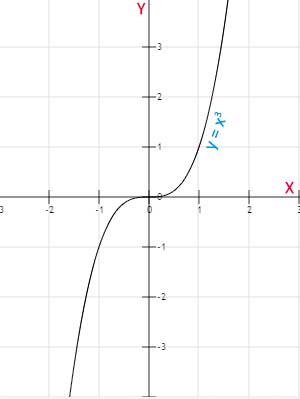
Función sin paridad: es aquella que no es par y tampoco es impar. Veamos un ejemplo de una función sin paridad:
Recuerda que puedes identificar la paridad de una función con ayuda de la gráfica, o verificando que se cumple la condición de paridad. En el video que viene líneas abajo, veremos algunos ejemplos.
Es importante mencionar que, si una función es par, entonces no puede ser impar. De la misma manera, si una función es impar, entonces no puede ser par. La única función que es par e impar a la vez es la función y=0.
Guía de ejercicios
A continuación, viene una guía con muchos problemas propuestos de funciones pares e impares, algunos de los cuáles resolveremos en el video, y otros quedarán para que puedas practicar en casa.
Funciones, ejercicios propuestos PDF
Video
En el siguiente video, realizaremos un breve repaso de las funciones pares e impares, y luego resolveremos diferentes ejercicios de paridad y simetrías de funciones.
Hasta aquí llegamos por ahora, si deseas, puedes revisar algunos temas adicionales de funciones en nuestro curso de cálculo.