Función lineal, ejercicios resueltos

Las funciones lineales son aquellas funciones que tienen la forma y = mx + b ; que también se pueden escribir de la forma f(x) = mx + b. Veamos algunas características importantes de la función lineal, junto a los ejercicios y aplicaciones que hemos preparado.

Elementos de la función lineal

En la función lineal, que siempre tiene la forma y = mx + b ; tenemos los siguientes elementos:

x: variable independiente.
y: variable dependiente (su valor depende del valor de x).
m: pendiente.
b: corte con el eje y, u ordenada de origen.

Veamos algunos ejemplos de funciones lineales y no lineales:

Cuando el valor de la pendiente (m) es igual a 0, nos encontramos ante un caso particular de la función lineal, que tiene el nombre de función constante.

Recuerda que, si se grafica una función lineal, siempre se obtiene una recta. Veamos la gráfica de la función y = 2x – 1.

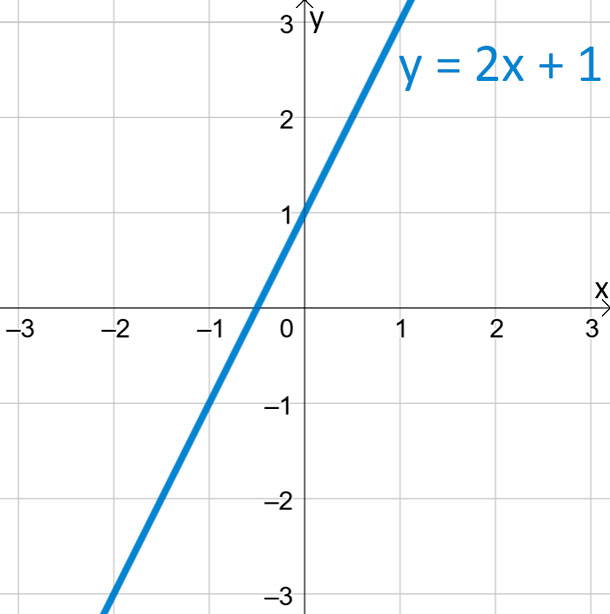
Pendiente en la función lineal

Veamos ahora la relación que existe entre la pendiente y el comportamiento de la función lineal.

Podemos apreciar que, de acuerdo al valor de la pendiente m, la función lineal puede ser creciente(m>0), decreciente(m<0), constante (m=0).

También es importante recordar que la pendiente se puede calcular a partir de dos puntos de la recta:

Dominio y rango de la función lineal

En una función lineal el dominio y rango siempre son los mismos, el conjunto de los números reales:

El único caso en que el rango no es el conjunto de los números reales, es el caso particular de la función constante, en el que “y” asume un único valor.

Ejemplo 1:

Calcular la pendiente de la recta 2y = 4x + 12

Solución:

Para obtener la pendiente «m», vamos a buscar la forma y = mx + b. Para ello, el coeficiente de y, pasará a dividir al segundo miembro:

A partir de esta igualdad, se obtiene el valor de la pendiente: m = 2.

Ejemplo 2:

Encontrar la ecuación de la recta que pasa por los puntos A = (2;3) y B = (6;5).

Solución:

Al ser una recta, sabemos que es la representación de una función lineal. Dado que tenemos dos puntos, diremos que A será el punto 1, y B el punto 2:

Primero, vamos a calcular la pendiente:

Ahora que ya tenemos el valor de la pendiente, reemplazamos en la ecuación de la función lineal para encontrar el valor del punto de corte con el eje y (b):