Titulo

Análisis dimensional, ejercicios resueltos

Análisis dimensional es el estudio o análisis de las relaciones entre diferentes magnitudes, identificando sus dimensiones y unidades de medida. Veamos algunos conceptos adicionales:

Magnitud

Es todo aquello que se puede medir.

Medir

Comparar una magnitud con otra magnitud de la misma especie. Por ejemplo, podemos realizar las siguientes mediciones:

• Si medimos la distancia de mi casa a la universidad, es de 300 metros. Aquí comparamos con el metro patrón.
• Si medimos la masa de mi cuerpo, es de 70 kg. Aquí comparamos con el kilogramo patrón.

¿Cómo se clasifican las magnitudes?

Las magnitudes se pueden clasificar de acuerdo a su origen y de acuerdo a su naturaleza.

Clasificación de las magnitudes

Por su origen: 1.       Magnitudes fundamentales. 2.       Magnitudes derivadas.

Por su naturaleza: 1.       Magnitudes escalares 2.       Magnitudes vectoriales.

Por su origen:

Magnitudes fundamentales:

Son aquellas elegidas magnitudes elegidas por convención, que permiten expresar cualquier física en términos de ellas.

En el sistema internacional, tenemos 7 magnitudes fundamentales:

Magnitudes derivadas:

Son aquellas magnitudes que se expresan en función de las magnitudes fundamentales. Por ejemplo: área, velocidad, fuerza, trabajo.

Las fórmulas dimensionales de las magnitudes derivadas son las siguientes:

Por su naturaleza:

Magnitudes escalares:

Son aquellas que enunciado su valor seguido de su correspondiente unidad quedan perfectamente definidas, a veces afectado de un signo negativo convencionalmente elegido. Por ejemplo:

• Longitud: 5 m.
• Temperatura: -12 °C.
• Tiempo: 5 s.

Entre las magnitudes escalares más utilizadas, tenemos: longitud, masa, tiempo, volumen, densidad, trabajo, potencia, energía, carga eléctrica, intensidad de corriente eléctrica, potencial eléctrico, iluminación.

Magnitudes vectoriales:

Son aquellas que además de conocer su módulo o valor, es necesario conocer su dirección y sentido para que esté plenamente definida.

Entre las magnitudes vectoriales más utilizadas, tenemos: desplazamiento, velocidad, aceleración, fuerza, potencia, torque, impulso, cantidad de movimiento, intensidad de campo eléctrico, inducción magnética.

¿Para qué sirve el análisis dimensional?

El análisis dimensional nos permite:

• Comprobar la veracidad de las fórmulas físicas mediante el principio de homogeneidad dimensional.
• Expresar las magnitudes derivadas en función de las magnitudes fundamentales.
• Determinar fórmulas empíricas a partir de datos experimentales.

¿Cómo se representa una magnitud física?

Sea A la magnitud física, entonces:
[A] : dimensión de la magnitud física de A.

Principio de homogeneidad dimensional

Si una fórmula física es correcta, entonces todos los términos de la ecuación o fórmula son dimensionalmente iguales. Por ejemplo:

Si: A = B + C/D
Entonces: [A] = [B] = [C/D]

Recuerda que sólo se pueden sumar magnitudes de la misma especie.

Ejercicio 1:

Hallar las dimensiones de z, sabiendo que x: masa, y que la siguiente ecuación es dimensionalmente correcta:

z = x + y

Solución:

Si la ecuación, es dimensionalmente correcta, entonces sus términos son dimensionalmente iguales (principio de homogeneidad dimensional).

[z] = [x] = [y]

Sabiendo que x: masa, entonces… [z] = M = [y]

Respuesta: [z] = M

Algunas propiedades del análisis dimensional

Propiedad de la suma y resta

Solo se puede sumar o restar magnitudes de la misma especie, y el resultado de dicha operación será igual a la misma magnitud:

L + L + L = L

M – M = M

Por otro lado, las reglas de multiplicación y división si se cumplen:

L‧L‧M = L2M

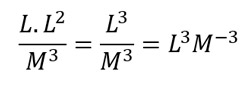
Ejercicio 2:

Encontrar la ecuación dimensional del potencial eléctrico V, sabiendo que:

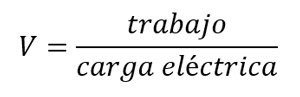
Solución:

Sabemos que:

• [trabajo] = ML2T-2
• [carga] = IT

Por ello:

Propiedad de los números

Los números son adimensionales. De manera práctica, la dimensión de un número es igual a 1. Incluimos en los números a: ángulos, funciones trigonométricas, funciones logarítmicas, constantes numéricas. Ejemplos:

• [5]=1
• [-8]=1
• [log25]=1
• [π]=1
• [30°]=1
• [sen60°]=1

También, se cumple para las raíces:

Ejercicio 3:

Si k=12mg(log5), hallar las dimensiones y unidades de k, sabiendo que la ecuación es dimensionalmente correcta. Además, m: masa, g: aceleración de la gravedad.

Solución:

k=12mg(log5)

[k]=[12][m][g][log5]

Como los números son adimensionales, entonces [12]=1; y también [log5]=1

[k]=1[m][g]1

[k]=1‧(M)‧(LT-2)‧1

[k]=MLT-2

Propiedad de los exponentes

Los exponentes son siempre números, por ello, la dimensión de un exponente se considera de forma práctica igual a 1.

Ejercicio 4:

En la siguiente fórmula física, encontrar las dimensiones de k, sabiendo que t: tiempo.

y = kekt

Solución:

Gracias a la propiedad de los exponentes, sabemos que estos siempre son números, por ello, su dimensión es igual a 1. En este caso, el exponente de «e» es k.t

Propiedad de los ángulos

Las funciones trigonométricas se aplican a los ángulos, los cuáles son números y se considera de forma práctica que su dimensión es igual a 1.

Ejercicio 5:

En la siguiente fórmula física, indicar la dimensión de w, sabiendo que A: longitud; t: tiempo.

x=wAsen(wt)

Solución:

En esta fórmula, vemos una función trigonométrica, la función seno. Las funciones trigonométricas, solo se aplican a los ángulos, los cuáles son números, y tienen dimensión igual a 1.

Guía de ejercicios

Para esta ocasión, tenemos una pequeña guía con muchos ejercicios propuestos, algunos de los cuáles resolveremos en los videos, y otros quedarán para que puedas practicar.

Análisis dimensional ejercicios propuestos PDF

Intro

En este primer video, veremos un poquito de teoría y luego algunos ejemplos muy interesantes:

Nivel 1A

En este video, veremos ejercicios sencillos así como la propiedad de los números. 

Nivel 1B

En este video, vamos a ver la propiedad de los exponentes y la propiedad de los ángulos. 

Nivel 2A

En este video vamos a resolver ejercicios de la regla de la suma y resta. 

Nivel 2B

En este video vamos a revisar 2 ejercicios muy interesantes de buen nivel. 

Nivel 3

Terminamos con un ejercicio que requiere conocer varias propiedades del análisis dimensional.

Tarea para la casa

Es tu turno para demostrar lo aprendido a lo largo de estos videos con los siguientes problemas:

Respuestas:

17.     x+y = 0

18.    [x] = ML3T-2