Media, mediana y moda para tablas sin intervalos
La media es el valor que se obtiene al sumar todos los datos multiplicados por su frecuencia y dividir el resultado entre la cantidad de datos. La mediana es el valor que ocupa la posición central si n es impar, y es el promedio de los dos datos centrales si n es par, cuando todos los datos están ordenados. La moda es valor con mayor frecuencia absoluta. Cuando buscamos encontrar la media, mediana y moda para datos agrupados sin intervalos o agrupados puntualmente, necesitamos realizar algunos pasos adicionales y conocer un par de fórmulas. Veamos como hacerlo.
Media
La media es el valor que se obtiene al sumar todos los datos multiplicados por su frecuencia y dividir el resultado entre la cantidad de datos. Usamos la siguiente fórmula:

Ejemplo 1:
Calcular la media de la siguiente distribución:
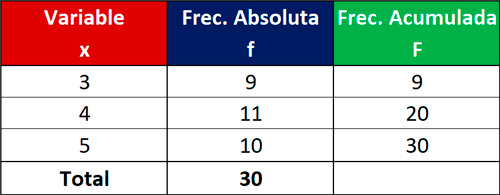
Solución:
Para calcula la media, vamos a agregar una columna adicional, en la que multiplicaremos el valor de la variable (x) por la frecuencia absoluta (f).

Recordamos la fórmula:

Mediana
La mediana es el valor que ocupa la posición central si n es impar, y es el promedio de los dos datos centrales si n es par, cuando todos los datos están ordenados.
Una manera rápida de encontrar la mediana, es encontrar el dato que ocupa la siguiente posición:

Y luego, ubicar dicho valor (x) a partir de la columna de frecuencias acumuladas.
Ejemplo 2 (n impar):
Calcular la mediana de la siguiente distribución:

Encontramos la posición del valor que está ubicado al centro:

Ahora, buscamos la posición 17 en la columna de frecuencias acumuladas:
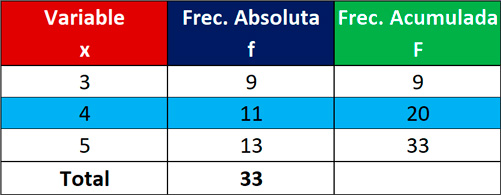
El valor (x) que ocupa dicha posición es 4, por lo tanto, Me = 4.
Ejemplo 3 (n par):
Calcular la mediana de la siguiente distribución:

Encontramos la posición del valor que está ubicado al centro:

Como nos ha quedado un valor con decimales, significa que la mediana será la media aritmética del valor que ocupa la posición 17, con el valor que ocupa la posición 18.
Buscamos los valores de posición 17 y 18 en la tabla de frecuencias acumuladas:

La posición 17, pertenece al valor x = 4, y la posición 18 también pertenece al mismo valor. Por lo tanto:

Ejemplo 4 (n par):
Calcular la mediana de la siguiente distribución:

Encontramos la posición del valor que está ubicado al centro:

Como nos ha quedado un valor con decimales, significa que la mediana será la media aritmética del valor que ocupa la posición 29, con el valor que ocupa la posición 30. Buscamos los valores de posición 29 y 30 en la tabla de frecuencias acumuladas:

El valor que ocupa la posición 29, es x = 4; mientras que el valor que ocupa la posición 30, es x = 5. Por lo tanto, la mediana sería:

Moda
La moda es el valor con mayor frecuencia absoluta.
Ejemplo 5:
Encontrar la moda de la siguiente distribución:

La moda es el valor con mayor frecuencia absoluta, así que ubicamos el mayor valor de frecuencia absoluta con su correspondiente valor de la variable x:

El valor con mayor frecuencia absoluta, es el 4, por lo tanto: Mo = 4.
Video
A continuación, viene el video que hemos preparado con muchos ejemplos y ejercicios resueltos.
Reto
Antes de ir a tu examen, intenta resolver el siguiente reto. La solución viene líneas abajo:

Solución:
Primero completamos la columna de frecuencias acumuladas:

Ahora, calculamos el producto de la columna de valor (x) por frecuencia absoluta (f) agregando una columna adicional a la tabla.

Ahora encontramos el valor de la media:

Para calcular la mediana, encontramos la posición central:

Ahora encontramos el valor que corresponde a la posición 13.

Por lo tanto, el valor de la mediana es: Me = 15.
Finalmente, calculamos la moda, teniendo en cuenta que es el valor con mayor frecuencia absoluta:

Por lo tanto, la moda es igual a: Mo = 17.


