Fracciones propias (con ejemplos)
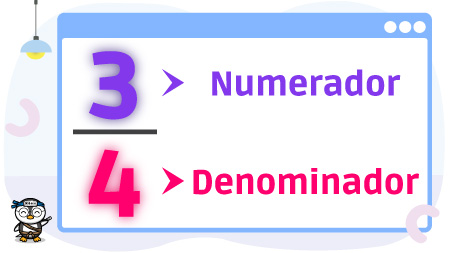
Hoy vamos a estudiar las fracciones propias. Ya verás que es un tema muy sencillo, lo único que tienes que recordar es que en una fracción, el numerador se ubica arriba y el denominador abajo.
Ahora sí, veamos qué es una fracción propia.
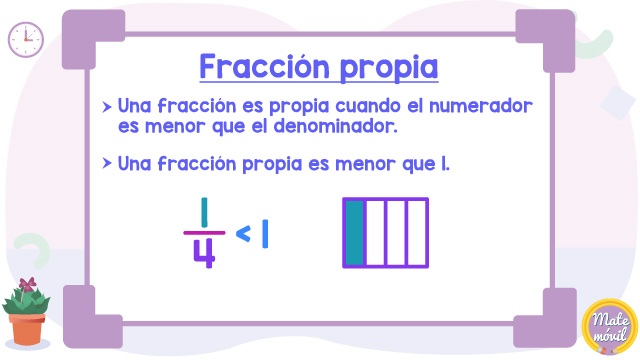
Fracción propia
Una fracción es propia cuando el numerador es menor que el denominador. Además, una fracción propia es menor que 1.
Ejemplo 1:
La fracción 1⁄4 es una fracción propia, pues el numerador 1 es menor que el denominador 4. También puedes comprobarlo graficando la fracción 1⁄4 , y verás que la fracción es menor que la unidad.

Ejemplo 2:
La fracción 2⁄3 es una fracción propia, ya que el numerador 2 es menor que el denominador 3. Además, puedes comprobar que la fracción es menor que 1 o menor que la unidad realizando su gráfica.

Ejemplo 3:
La fracción 5⁄6 es una fracción propia, pues el numerador 5 es menor que el denominador 6. También puedes comprobarlo graficando la fracción 5⁄6 , y verás que la fracción es menor que la unidad (1).

10 ejemplos de fracciones propias:
Las siguientes fracciones también son propias, pues su numerador es menor que el denominador: 3⁄4; 6⁄7; 5⁄8; 1⁄2; 3⁄5; 5⁄7; 7⁄8; 30⁄41; 11⁄12; 100⁄101.
Ejercicios
Indicar si las siguientes fracciones son propias o no.
a) 3⁄3
b) 4⁄5
c) 5⁄4
d) 17⁄18
Solución:
a) No es una fracción propia.
b) Si es una fracción propia.
c) No es una fracción propia.
d) Si es una fracción propia.
Video
En el siguiente video, te cuento un poco más sobre las fracciones propias.
Te cuento un poco más
Si quieres aprender sobre las fracciones iguales a la unidad y las fracciones impropias, puedes entrar aquí.
Referencias
Para esta clase hemos usado las siguientes referencias:
- Baldor, A. (2017). Aritmética (3.ª ed., pp. 234-235). Grupo Editorial Patria.
- Tussy, K., Gustafson, D. y Koenig, D. (2013). Matemáticas básicas (4.ª ed.; pp. 209, 217). Cengage Learning.
- Santillana Perú (2019). Resuelve: matemática 5° de primaria (p. 44).


